The Dynamics of Conflict. Technology, Hegemony, Balance of Power and Buffer States
In a recent paper[1] we propose a simple model to study the dynamics of conflict. Our analysis illuminates a number of strategies and concepts in international relations and military history.
The game
We consider a set of players – think leaders of nations – who are positioned on the nodes of a fixed network. A link of the network
represents a potential avenue for conflict between the two players it connects: a border for instance. Each node is endowed with a fixed resource: a nation’s wealth. The player controlling the node controls its resource.
We assume players maximise their utility, that is they maximise the resources they control. We model a Hobbesian anarchy: the only way of taking control of additional resources is by capturing the nodes of neighbouring players through conflict.
Conflict is modelled as a contest. When player A attacks player B then the probability that A wins the contest is determined by a contest success function (CSF): the probability of winning depends on the technology of conflict and on resources of the opponents. The winner of the contest takes over the nodes and resources controlled by the loser. Figure 1 provides an example.
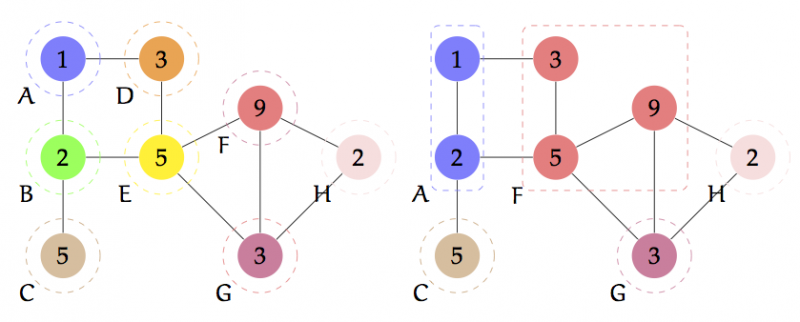
Figure 1: Player A attacks player B and wins the conflict. Player F wins against D and E. This changes players’ ownership of nodes as well as resources (here denoted by integers) and potentially brings them into contact with new neighbours.
A player can choose between two courses of action: staying peaceful and engaging in a sequence of conflicts. At each point in the sequence the consecutive opponent must own a node neighbouring one of the nodes currently controlled by the attacking player.
The game proceeds in rounds. If all players choose to be peaceful at a given round or if only one player is left, then the game ends. Otherwise one of the players choosing a fighting sequence is picked at random and implements her fighting strategy. A round finishes either if the player wins all fights in her sequence, or if she loses a conflict. Since the number of players is finite the game must end eventually.
The technology of conflict plays a key role in our study. Two cases are identified: strong rewarding and weak rewarding CSF. The CSF is strong rewarding if in a pair the stronger player (i.e., one with more resources) has an expected payoff from conflict exceeding her initial resources. Respectively, the CSF is weak rewarding if in a pair the weaker player has an expected payoff from conflict exceeding her initial resources. Unless mentioned otherwise we focus on the strong rewarding CSF.
We introduce the notion of strong players: players who have a fighting sequence involving every other player in which the attacker is the stronger player, in every conflict, along the sequence. The player with most resources is always strong. Figure 2 demonstrates this notion.
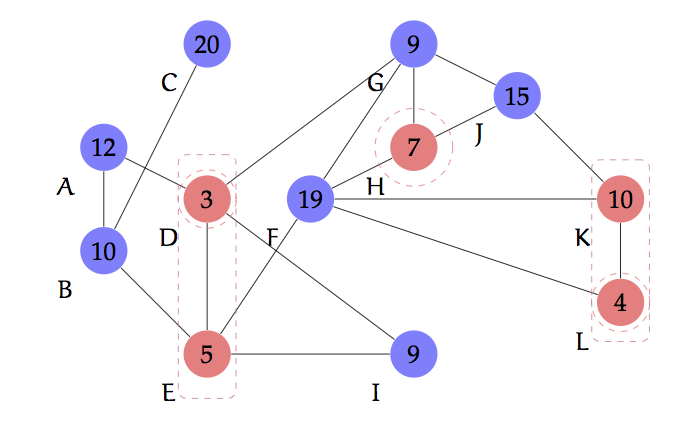
Figure 2: Players in blue are strong and players in pink are weak. Notice that geography matters: player K has more resources than G, but is weak.
Hegemony and pre-emption
We show that there exists a unique equilibrium outcome: hegemony obtains. This result is driven by two factors. Firstly, conflict increases the expected resource holdings of a strong player. Secondly, for all players it is always better to attack than to wait for other players to have engaged in conflict with each other: waiting only leads to stronger opponents. Hence strong players have a dominant strategy of choosing a full fighting sequence.
Weak players make a pre-emptive attack: they realize that continual conflict is imminent and maximize their payoff by choosing an optimal attacking sequence. Hence, players who would prefer peace if everyone else was peaceful opt for conflict. Walzer (1978) puts forward three conditions which he believes need to be satisfied to justify a pre-emptive war:
...a manifest to injure, a degree of active preparation that makes that
intent a positive danger, and a general situation in which waiting, or
doing anything other than fighting, greatly magnifies the risk.
Walzer (1978), Chapter 5
The considerations of weak players in our game fit precisely with the third point: waiting will make them strictly worse off.
Monotonic Attack
We show that it is optimal to attack opponents in increasing order of size. This way the size difference between own and opponent’s
resources is maximized in each attack which is to the attacker’s advantage. Attacking larger opponents first would lead to a greater payoff upon winning and hence greater strength in future fights, however this is not compensated for by the smaller probability of winning the fight against a larger opponent.
In the discussion so far we have assumed that conflict is efficient: there is no waste of resources. In reality conflict is often extremely wasteful. Suppose each conflict leads to a loss of δ ∈ (0, 1) of the total resources employed in each conflict. Different types of outcomes arise. For sufficiently low costs of conflict (low δ), the hegemony result remains unchanged. For sufficiently high costs of conflict no player ever attacks another. For intermediate costs of conflict, we obtain a number of new insights. We discuss one of them next.
Buffer states
With costs of conflict there can exist weak players who control so few resources that an attack is not worthwhile for any neighbouring
strong player. If such a player separates two larger players she can cause peace in an otherwise conflictual environment: she is a buffer state[2]. The example in figure 3 demonstrates this idea.
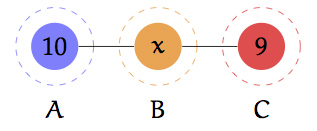
Figure 3: Fix the technology of conflict such that the larger player in a pair always wins conflict and set δ = 0.4. If x ≤ 5 then B acts as a buffer state: there is peace. If x > 5 then there is fighting to hegemony. Note, that if there was a link between players A and C then there could not be peace and that B is always neutral: it never attacks any other player.
If a large player were to deviate and attack the buffer state then this would be followed by an attack of her remaining opponent, the other large player.
There exists a growing literature on buffer states. A substantive discussion including a list of examples of such states is provided by Ross and Chay (1986) who attribute three characteristics to them:
...they are small countries, in both area and population; they are adjacent
to two larger rival powers; and they are geographically located
between these opposing powers.
Ross and Chay (1986), Chapter 1
In the discussion so far we have focused on the strong rewarding CSF. We conclude our discussion with a concept which requires a weak rewarding CSF.
Balance of power
With costs of conflict and a weak rewarding CSF it is possible that each bilateral conflict in any sequence of fights is not profitable
for either side. In particular, we show that for any star network, any weak rewarding CSF and any resource endowment such that the ratio of smallest to largest resource is strictly larger than 1 - δ peace is an equilibrium outcome. Hence with a sufficiently uniform resource endowment a balance of power can be attained. Uniformity in resources can be relaxed the larger the costs of conflict.
Balance of power is widely discussed in international relations. It is sometimes defined as ‘an equilibrium of power sufficient to discourage or prevent one nation or party from imposing its will on or interfering with the interests of another’ (Merriam-Webster Dictionary). The concept is of particular historic relevance in Europe. The basic idea is that no single European power – state or alliance of states – should be allowed to achieve hegemony. This is attained by carefully arranging alliances so to achieve a balance of power. Kissinger (2014) argues that a ‘balance of power that enforces restraint where rules break down’ must be part of any ‘world order’.
[1] For a short version follow: http://doi.acm.org/10.1145/2940716.2940776.
[2] The Oxford Dictionary defines a buffer state as a ’small neutral country situated between two larger hostile countries and serving to prevent the outbreak of regional conflict’.
References
- Kissinger, Henry (2014), World Order. Penguin Press.
- Ross, Thomas E. and John Chay, eds. (1986), Buffer States in World Politics.
- Walzer, Michael (1978), Just and Unjust Wars. Basic Books.
About the Authors

Marcin Dziubiński is an assistant professor at Institute of Informatics, Warsaw University. His research interests concentrate around economics and computation, including networks, conflicts on multiple battlefields, and location games.
Sanjeev Goyal is Professor of Economics at the University of Cambridge and Fellow of Christ's College, Cambridge. He is a pioneer and leading international scholar in the study of social and economic networks. His book, `Connections: an introduction to the economics of networks`, was published in 2007 by Princeton University Press. A Chinese translation appeared in 2010.
Sanjeev Goyal is a Fellow of the British Academy and was the Founding Director of the Cambridge-INET Institute.
 David Minarsch is a PhD student in Economics at the University of Cambridge. His work focuses on investigating traditional microeconomic topics in the context of social and economic networks. His models make the relationship structure between economic agents explicit and analyse its impact on economic outcomes. His PhD thesis has two broad topics: intermediation in networked markets and conflict.
David Minarsch is a PhD student in Economics at the University of Cambridge. His work focuses on investigating traditional microeconomic topics in the context of social and economic networks. His models make the relationship structure between economic agents explicit and analyse its impact on economic outcomes. His PhD thesis has two broad topics: intermediation in networked markets and conflict.

