The International Sharing of Stem Cells

Bone marrow transplants dramatically improve survival prospects of leukemia patients. However, for transplants to work, the donor must be a genetic match for the recipient. Only 30 percent of patients have a matching sibling. The rest must find a match among the general population.  The matching problem is difficult with more than half the population of a genetic type that matches fewer than 1 in 100,000 (Bergstrom et al., 2009).  The traditional solution to this problem has been to record the genetic types of potential donors in a registry.

The first bone marrow registries were established around 40 years ago. Shirley Nolan established The Anthony Nolan Register for her son in London, England in 1974. Currently there are 100 registries in 57 countries, 25 of which have over 100,000 registrants. The countries with the largest registries are the United States with over 8.5 million, Germany with approximately 6.5 million, Brazil with 3.9 million, China with 2.2 million, and the United Kingdom with just over 1.1 million. There are currently over 28.6 million registrants worldwide.[1]

In many instances a match for a needy patient cannot be found on the registry of the patient's home country. In such cases doctors may search the registries of other countries. These searches are done using an international data base maintained by Bone Marrow Donors Worldwide.[2]

Sharing of stem cells is also facilitated by partnerships. The National Marrow Donor Program (NMDP) in the United States maintains donor information for registries in the United States, Germany, Israel, Netherlands, Norway, and Sweden. The NMDP is the largest registry and historically its member countries have accounted for nearly 70 percent of international stem cell shipments.

The likelihood that two individuals will be a genetic match varies by race.  While two people are more likely to match if they are of the same race, the probability of matches across races is not negligible.  Table 1 provides matching probabilities by race for four broad racial categories.[3] The matching probabilities depend upon the genetic diversity of the races. Because the African American population is much more heterogeneous than the Caucasian population, the probability that two randomly selected African Americans have matching types is about one-tenth of the corresponding probability for Caucasians. Likewise, the cross-race matching probabilities are always smaller than the corresponding within-race probabilities.

Table 1: Entries give the probability that a randomly selected member of the row race matches a randomly selected member of the column race.

What this means is that bilateral frequencies of international shipments of stem cells should depend upon the racial compositions of the associated country pairs. In particular, absent a home bias or other structural factors, stem cell flows between countries with similar racial compositions should be expected to follow a hypergeometric distribution; accounting for the aggregate number of stem cells countries import and export, the network of bilateral flows should look as if there were randomly determined.

However, casual inspection of the data suggests that this is not the case. In recent years there have only been three big players in the export business. These are the United States, Germany, and the United Kingdom. In fact, more than two-thirds of the world's exports of transplants come from German donors. Despite its large registry, the United States imports about 45 percent of the units that it transplants.

In ongoing work by Garratt, Hayes and Mantegna (2016), henceforth GHM, the authors apply a hypergeometric test to observed flows of stem cells between countries to see which flows are statistically validated (Tumminello et al., 2011).  Statistically validated flows are either too large or too small to have occurred if all flows were truly random assuming the heterogeneity of flows observed in real data. Thus statistically validated flows provide indications of genetic differences across countries or structural factors the positively or negatively impact flows.   

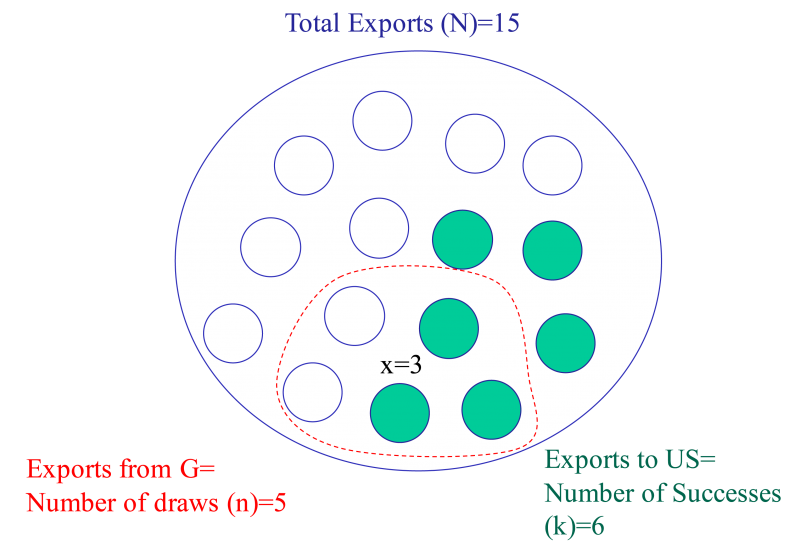
The logic behind the hypergeometric test is illustrated in Figure 1. The figure depicts a world with N=15 total exports represented by the 15 circles in the ring. The k=6 green colored circles are exports to a particular country, say the US. Think of these as successes. The hypergeometric test asks the question: Given that some country G exports n=5 stem cells in total (think of this as the number of draws without replacement; the collection captured by the red-dashed line indicates one possible outcome of 5 draws) what is the likelihood of observing at least or no less than x successes, depending on the type of test, where x is the actual number of exports from G to the US.

The GHM study uses country-level data on exports and imports of stem cells (marrow and apheresis) provided by the WMDA in their 2009 and 2013 annual reports and applies the methodology used to obtain statistically validated networks against a null hypothesis introduced in (Tumminello et al., 2011) and adapted to repeated directed interactions in (Li et al., 2014, Hatzopoulos et al., 2015).

Figure 2 shows the inflows and outflows and stem cells from countries of European Descent. Flow direction is clockwise. The figure reveals large flows from Germany to the United States and the United Kingdom and to itself. There are no correspondingly large inflows to Germany. What is not clear from this diagram is whether or not these flows are extraordinary. That is, are they greater or smaller than what we would expects if there were no genetic or structural factors impacting flows?

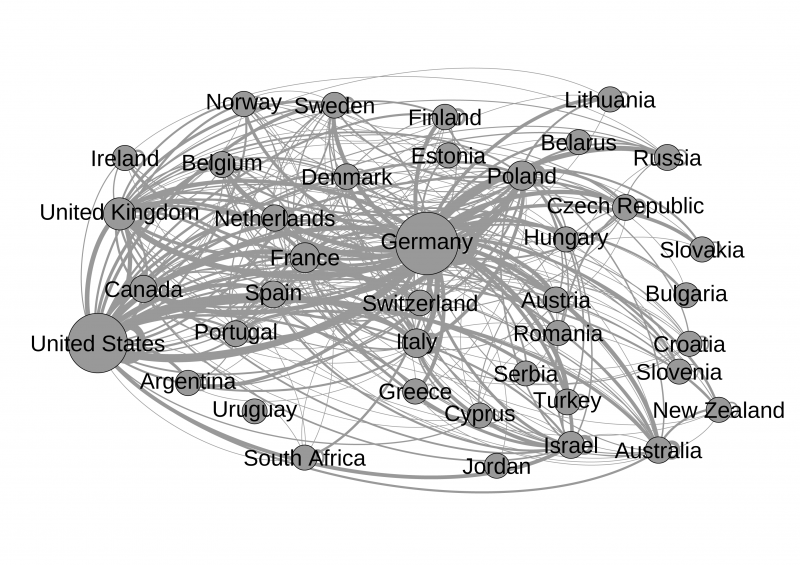
Figure 2: Weighted flows of stem cells for 2013. Countries of European descent.

Figure 3 shows links that are statistically over-expressed. These flows are so large that it is very unlikely that would have occurred randomly.[4] We see that the large flows from Germany to the US and UK, shown in figure 2, are in fact not statistically exceptional. However, the level of flows from Germany to France, the Netherlands, Belgium, Denmark, Russia and Turkey are significantly over-expressed. Own flows to the US, Germany and the United Kingdom, among other countries, are also exceptionally large, indicating a home bias.

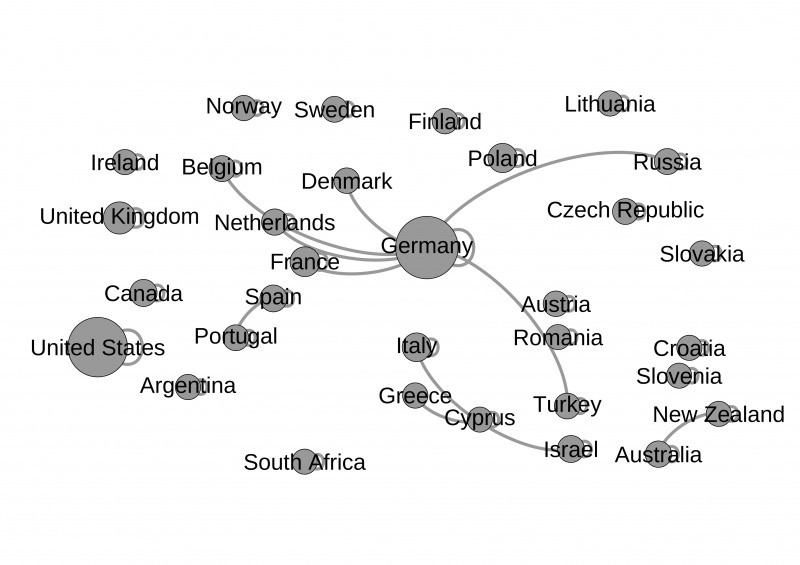
Figure 3: Statistically validated over-expressed links.

Finally, Figure 4 shows links that are statistically under-expressed. These flows are smaller than ones that would have been expected to occur randomly assuming the heterogeneity of flows observed between pairs of countries. The take-away from this figure is that both Germany and the US export too few stem cells to multiple countries. In the case of Germany, there seems to be some selection going on. They over export to some countries and under export to others. In contrast the US’s only over expressed link is to itself.

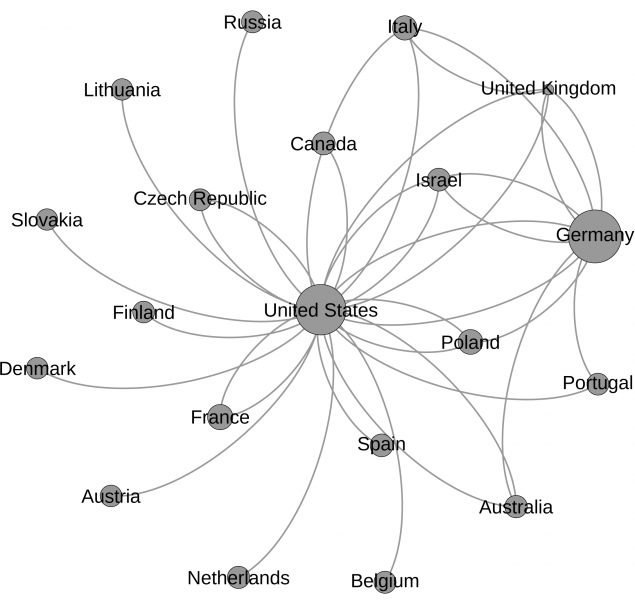
Figure 4: Statistically validated under-expressed links.

 References

• Bergstrom, T. C., R. J. Garratt and D. Sheehan-Connor. 2009. One Chance in a Million: Altruism and the Bone Marrow Registry, American Economic Review, 99(4), pp. 1309-34.
•  Bergstrom, T. C., R. J. Garratt and D. Sheehan-Connor. 2012. Stem Cell Matching for Patients of Mixed Race. The B.E. Journal of Economic Analysis & Policy. 12(1), ISSN (Online) 1935-1682, DOI: 10.1515/1935-1682.3275.

•  Garratt, R. J., R. Hayes and R. Mantegna. 2016. The International Sharing of Stem Cells. Mimeo.

•  Li, M.X., Palchykov, V., Jiang, Z.Q., Kaski, K., Kertész, J., Miccichè, S., Tumminello, M., Zhou, W.X. and Mantegna, R.N., 2014. Statistically validated mobile communication networks: the evolution of motifs in European and Chinese data. New Journal of Physics, 16(8), p. 083038.

•  Hatzopoulos, V., Iori, G., Mantegna, R.N., Miccichè, S. and Tumminello, M., 2015. Quantifying preferential trading in the e-MID interbank market. Quantitative Finance, 15(4), pp. 693-710. 
• Tumminello M, Miccich S, Lillo F, Piilo J, Mantegna RN (2011) Statistically Validated Networks in Bipartite Complex Systems. PLoS ONE 6(3): e17994. doi:10.1371/journal.pone.0017994.

Rod Garratt holds the Maxwell C. and Mary Pellish Chair in Economics at the University of California Santa Barbara. He is a theorist who specializes in applied game theory. He is known for his work on strategic incentives in payment systems and has consulted on payment systems for the Bank of Canada, Payments Canada, the Bank of England, the Federal Reserve Bank of New York, De Nederlandsche Bank and the Central Bank of Serbia. He was a Research Advisor at the Bank of England from 2009-2010 and was a Vice President in the Money and Payments Studies division of the Federal Reserve Bank of New York from 2013-2015. From 2014-2015 he co-lead the Virtual Currency Working Group for the Federal Reserve System. In addition to numerous works on large value payment systems, Garratt has published theoretical and experimental work related to auctions and helped develop a growing literature on the role of speculators in auctions with resale. He also pioneered the use of information-theoretic clustering techniques to describe behavior and identify risks in complex financial networks. Garratt received his undergraduate degree form the University of Waterloo and his Ph.D. from Cornell University. He has published in the top economics journals including Econometrica, the American Economic Review and the Journal of Political Economy. He is an Associate Editor of the Journal of Financial Market Infrastructures, the Journal of Network Theory in Finance and the Journal of Public Economic Theory. He has held visiting positions at the University of Arizona and UCLA. He is currently an Advisory Board Member of R3 CEV.