Kidney Exchange: an Application of Matching Theory and Mechanism Design
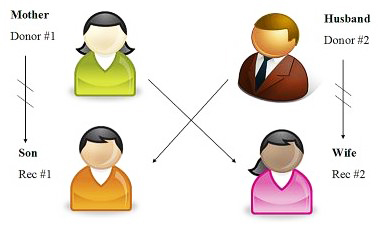
A kidney exchange problem consists of a set of incompatible patient-donor pairs together with a profile of ordered lists of all donors' kidneys, one list for each patient. A patient's ordered list of all kidneys (from the best to the worse) reflects, according to the patient's nephrologist, the ex-ante ordinal quality of the match between each kidney and the patient. The mechanism design question is to determine a systematic way of selecting, for each kidney exchange problem, a set of compatible transplants with desirable properties. Three economists, A. Roth (at Harvard University), T. Sönmez, and U. Ünver (both at Boston College), published in 2004 a paper in The Quarterly Journal of Economics studying the kidney exchange problem and proposing an adaptation of an already known algorithm in matching theory to solve all kidney exchange problems. The algorithm is known as the Gale's Top Trading Cycle Algorithm, and I will refer to it as the TTC algorithm.
Given a kidney exchange problem (remember, a set of incompatible patient-donor pairs and a profile of patients' lists, each list ordering all present donor's kidneys) the TTC algorithm solves the problem (i.e., proposes a set of compatible transplants) in stages. At each stage, the TTC algorithm roughly works as follows. (1) It constructs a graph whose nodes are the patient-donor pairs that have not yet been matched in the previous stages; (2) it directs the graph (a single arrow leaves from each node pointing to another node) by making that the patient points to the best kidney (according to his ordered list of kidneys) among those still present in the stage; (3) it identifies the nodes on the cycles of the directed graph; and (4) it satisfies the cycles, matching each patient of the nodes of the cycles to his pointed kidney.
The TTC algorithm keeps identifying and satisfying successively the cycles along the stages. Note that in each stage, there is always at least one cycle, if there are several cycles they do not intersect each other and a cycle may have a single node whose patient points to the kidney of his donor (obviously, since they are not compatible, the patient in this case will not be transplanted and the patient will remain under dialysis). Thus, the input of the TTC algorithm is an instance of a kidney exchange problem and its output is a solution of the problem that consists of a proposal of transplants based on the cycles identified along its stages. The TTC algorithm has many desirable properties. First, it is individually rational: every patient that receives a kidney at the outcome of the TTC algorithm prefers this situation rather than not receiving a kidney and remaining under dialysis. Second, it is efficient: all patients can not improve simultaneously; that is, if there is another set of transplants where one patient receives a strictly better kidney then, there must exist another patient that receives a strictly worse kidney. Third, the output of the TTC algorithm belongs to the Core of the kidney exchange problem: there is no subset of patient-donor pairs that, by reassigning the kidneys of the donors only among the patients in the subset, can obtain better kidneys; that is, no group of patient-donor pairs (for example those from a hospital, a city or a region) can object unanimously to the output of the TTC algorithm. Moreover, the Core of each kidney exchange problem is unique and coincides with the output of the TTC algorithm. Fourth, the mechanism associated to the TTC algorithm is strategy-proof: no patient could obtain a strictly better kidney by reporting (in fact, his nephrologist) a false ordered list of kidneys. Furthermore, the mechanism that, for each kidney exchange problem, selects the output of the TTC algorithm is the unique individually rational, efficient, and strategy-proof mechanism. Finally, the quality of the kidney received by each patient in the output of the TTC algorithm depends positively on the quality of his kidney's donor.
Finally, Roth, Sönmez, and Ünver (QJE, 2004) also reports some simulations suggesting that the TTC algorithm performs well and that it can be applied to real kidney exchange problems, and indeed it is now used in most countries with kidney exchange programs. But in addition, the paper has also triggered an already long list of papers studying different issues related to the specific nature of the kidney exchange problem that may require to adapt the TTC algorithm. For instance, (1) to deal with the increasing number of altruistic donors (called "good samaritans"), whose kidney can be used to initiate chains (instead of cycles) of transplants; The New York Times, on February 18, 2012 contained an article entitled 60 Lives, 30 Kidneys, All Linked describing a chain of 30 transplants initiated one year earlier by a good samaritan. (2) The consequences of requiring alternative incentive properties (weaker than strategy-proofness) when patients (their nephrologists) submit the ranked list of all donors' kidneys. (3) The presence of patients with several potential donors. (4) Ethical issues related with the ex-ante worse situation faced by O blood type patients since they can only receive kidneys from O blood type donors. (5) The effects of considering explicitly the dynamic feature of the problem, where the database of pairs keeps changing by the entrance and exit of patient-donor pairs.
In any case, kidney exchange has become a natural and successful application of Matching Theory and Mechanism Design to help human beings to live longer and better.
About the Author
 Jordi Massó Carreras is a Professor of Economics at the Universitat Autònoma de Barcelona and a member of Markets, Organizations and Votes in Economics (MOVE) since 2009.
Jordi Massó Carreras is a Professor of Economics at the Universitat Autònoma de Barcelona and a member of Markets, Organizations and Votes in Economics (MOVE) since 2009.
Jordi Massó works on Mechanism Design, a research area in the intersection of Game Theory and Social Choice Theory, which deals with the study and design of institutions (mechanisms) with the aim of helping societies to take collective decisions. The emphasis is not only on the normative properties of the mechanism (for instance efficiency and equity) but also on the strategic incentives they induce on agents. Recently, he has been applying mechanism design tools to study three different classes of problems: matching, voting, and the allocation of a divisible good.
Contact: jordi.masso@uab.es
